与你交谈系列#2

介绍

今天我们将开始概述用于解决各种算法问题的概念。对某个概念的理解可能会给你一个直觉，从哪个角度开始思考潜在的解决方案。

有不同但没有太多的概念。今天我将把你的注意力集中在滑动窗口概念上。

滑动窗口

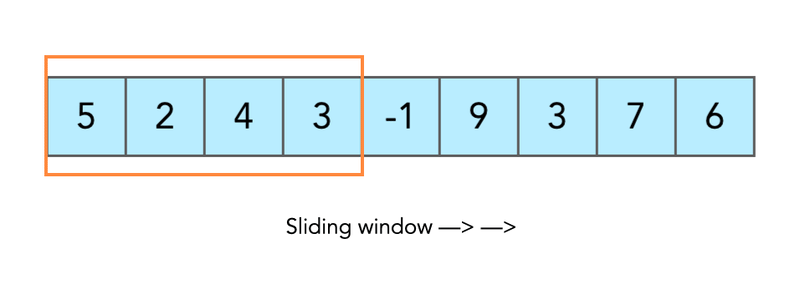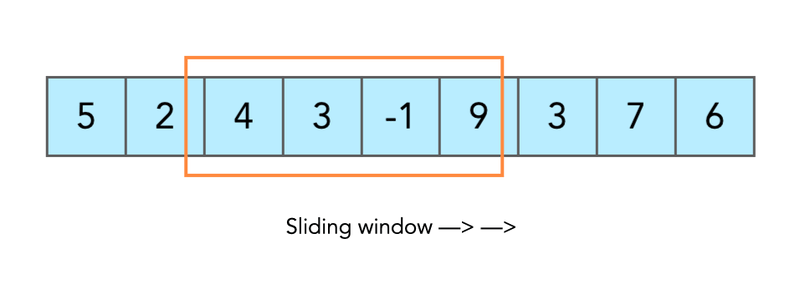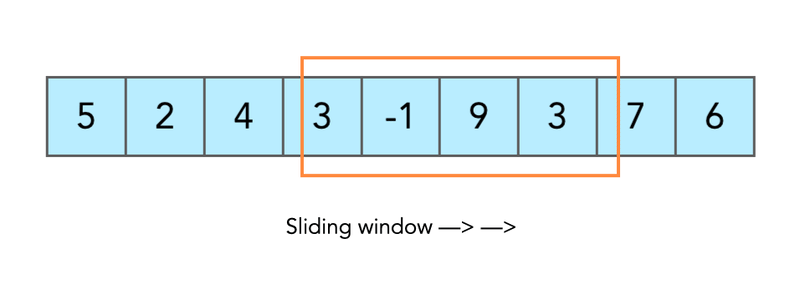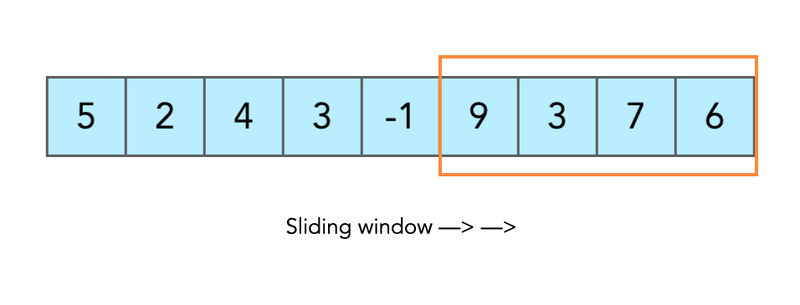
与你交谈系列#2

滑动窗口的概念比乍一看要复杂一些。我将通过实际例子来证明这一点。现在，请记住，概念性的想法是我们将有一些必须移动的窗口。让我们立即从示例开始吧。

假设您有一个整数数组和预定义的子数组大小。你被要求找到这样一个子数组（又名窗口），其值的总和将是最大的。

array = [1, 2, 3]
window_size = 2

# conceptually
subarray_1 = [1, 2] --&gt; sum 3
subarray_2 = [2, 3] --&gt; sum 5

maximum_sum = 5

登录后复制

嗯，看起来很简单：
(1) 尺寸为 2 的滑动窗
(2) 2 个子数组
(3) 计算每一项的总和 (4) 找出它们之间的最大值

让我们实现它吧。

def foo(array: list[int], size: int) -&gt; int:
    maximum = float("-inf")

    for idx in range(size, len(array)+1):
        left, right = idx-size, idx
        window = array[left:right]
        maximum = max(maximum, sum(window))

    return maximum

登录后复制

嗯，看来我们刚刚有效地使用了滑动窗口的概念。事实上，不完全是。通过了解解决方案的时间复杂度，我们可以得到“证明”。

复杂度为 o(l)*o(w)，其中 l 是数组中窗口的数量，w 是窗口中元素的数量。换句话说，我们需要遍历l个窗口，对于每个第l个窗口，我们需要计算w个元素的总和。

这里有什么问题吗？让我们概念性地描述回答问题的迭代。

array = [1, 2, 3, 4]
window_size = 3

iterations
1 2 3 4 5
|___|
  |___|
    |___|

登录后复制

答案是，即使我们滑动数组，在每次迭代中我们都需要“重新计算”在上一次迭代中已经计算过的 k-1 个元素。

基本上，这种见解应该建议我们提出一个问题：

“有没有办法利用上一步的计算？”

答案是肯定的。我们可以通过将窗口元素的第一个和下一个元素相加和相减来得到窗口元素的总和。让我把这个想法写入代码中。

def foo(array: List[int] = None, size: int = 0) -&gt; int
    window_start, max_, window_sum_ = 0, float("-inf"), 0
    for window_end in range(len(array)):
        if window_end &gt; size - 1:
            window_sum_ -= array[window_start]
            window_start += 1
        window_sum_ += array[window_end]
        max_ = max(max_, window_sum_)
    return max_

assert foo(array=[1, 2, 3, 4], size=3) == 9

登录后复制

在这里我们可能会看到，当我们构造长度为 size 的子数组时，我们开始从窗口总和中减去第一个元素，这使得我们可以重用上一步的计算。

现在，我们可以说我们有效地利用了滑动窗口的概念，同时我们得到了检查时间复杂度的证明，时间复杂度从 o(l*w) 减少到 o(l)，其中 l 是我们将滑动的窗口数量。

我想强调的主要思想，滑动窗口概念不仅仅是用特定大小的窗口来切片可迭代对象。

让我给你一些问题，我们将学习如何检测问题可能涉及滑动窗口概念以及你到底可以对窗口本身做什么。

问题概述

由于我在这里只讨论概念，因此我会跳过“如何计算窗口内的某些内容”。

问题一

给定一个数组，求其中所有大小为 k 的连续子数组的平均值。

好，现在我们可以这样定义该方法：使用大小为 k 的窗口迭代输入数组。在每次迭代中计算窗口的平均值...

问题二

给定一个正数数组和一个正数 k，找到大小为 k 的任何连续子数组的最大和。

现在：使用大小为 k 的窗口遍历输入数组。在每次迭代中计算窗口的总和...

问题三

给定一个正数数组和一个正数 s，找到总和大于或等于 s 的最小连续子数组的长度。

现在，我们可以这样定义该方法：“首先，迭代输入数组并构造这样的第一个窗口，它将满足条件（总和为 >= 到 s）。完成后，移动窗口，管理窗口开始和结束...”

问题四

给定一个字符串，找到其中不超过 k 个不同字符的最长子字符串的长度。

这里的方法有点复杂，所以我在这里跳过。

问题五

给定一个整数数组，其中每个整数代表一棵果树，给你两个篮子，你的目标是在每个篮子里放入最大数量的水果。唯一的限制是每个篮子只能放一种水果。
你可以从任何一棵树开始，但一旦开始你就不能跳过一棵树。您将从每棵树上采摘一种水果，直到您无法采摘为止，也就是说，当您必须从第三种水果中采摘时，您将停止。
编写一个函数来返回两个篮子中水果的最大数量。

好像不是那么明显，我们先简化一下条件。